日期：2026年 01月 31日

標籤： Algorithm String Searching Algorithm C# Asp.NET Core

摘要：演算法-字串搜尋

第一部分：Z 演算法 - 介紹

Step 1：簡介

以下截取於GeeksforGeeks（GfG）平台

In many programming problems involving strings, we often need to search for occurrences of a pattern inside a text. 
A classic approach like the naive string matching algorithm checks for the pattern at every index of the text, 
leading to a time complexity of O(n·m),
where n is the length of the text and m is the length of the pattern. 
This is inefficient for large inputs.

To address this, several efficient string matching algorithms exist one of them is the Z-Algorithm, 
which allows us to perform pattern matching in linear time. That means, it can find all matches in O(n + m) time.

簡言之，搜尋一串字串(文本)，用此演算法可以在線性時間內 O(n+m) 完成
※來源：Wiki

Step 2：優缺點

優點具有以下：

1. 保證線性時間複雜度 O(N+M)	：	無論文本、搜尋字串為何，永遠都為 O(N+M)
2. 實作相對簡單	：	代碼可讀性與實作容易，將 Z演算法陣列全部匹配計算完成即可
3. 一次預處理，多次查詢	：	文本 + “#” + “搜尋字串” 搞定，極高效預處理
5. 空間局部性好	：	演算法主要是順序掃描，對 CPU Cache 友好

缺點：

1. 空間複雜度較高 O(N+M)	：	如果文本 + 搜尋字串要 2GB 記憶體空間，那麼開銷至少要 4GB 記憶體空間才能執行
2. 無法進行串流處理	：	需要完整的搜尋字串、文本才能開始此演算法，KMP 就可以逐步執行
3. 對於非常短的模式，額外開銷較大	：	文本少時，搜尋字串越長，建立陣列開銷大
4. 不支援模式的動態修改	：	不同的搜尋字串、文本都需要重建陣列
5. 對於部分場景不是最優	：	不能模糊匹配，只能精確匹配

Step 3：常見的字串搜尋演算法 - 比較分析

特性	Z 演算法	KMP	Boyer-Moore	暴力搜尋
時間複雜度	O(N+M)	O(N+M)	O(N/M) ~ O(N*M)	O(N*M)
空間複雜度	O(N+M)	O(M)	O(M)	O(1)
實作難度	中等	中等	較難	簡單
直觀性	高	中	低	高
串流處理	不支援	支援	支援	支援
多模式搜尋	不適合	不適合	不適合	不適合

高效能 + 可讀性高 有不可取代性，在極小專案中可以快速實現不算差的匹配搜尋，但是遠遠不適合在企業級應用中使用。

Step 4：應用場景建議

基本上除了理解匹配應用、小型專案外，不建議使用此字串演算法，有更多優秀有效的演算法應用

適合的場景	不適合的場景
1. 學術研究和教學（理解字串匹配原理）	1. 處理巨大文件且記憶體有限
2. 需要保證最壞情況性能的場合	2. 需要串流處理數據
3. 一次性搜尋，不需要串流處理	3. 搜尋多個不同的模式
4. 記憶體充足的環境	4. 對空間效率要求極高
5. 需要額外利用 Z 陣列信息（如週期性分析）	5. 企業級應用（通常用更優化的演算法）

第二部分：Z 演算法 - 實現

Step 1：完整代碼

完整代碼可以從Source Code下載，此代碼對應於 LeetCode 的 796 題，Prime Number of Set Bits in Binary Representation

主要以下 6 個步驟完成，完整代碼如下：

步驟	說明
1~3	預處理，z 演算法需要的準備工作，分隔符號必須是 text , pattern 不存在的字符
4~6	將 zBox 陣列的每個匹配完成，最終 zBox 可以計算出與 pattern 比對相同字元數量
匹配函式	字元與字元的比對

private bool ZAlgorithmSearch(string text, string pattern)
{
    // 1. 將模式、分隔符、文本組合成一個字串 (分隔符這邊用 # 要避免與匹配字串影響)
    var searchStr = $"{pattern}#{text}";

    var searchLength = searchStr.Length;// 組合字串的總長度
    var modelLength = pattern.Length;   // 模式字串的長度（用於後續判斷是否完整匹配）

    // 2. 初始化 Z 陣列 
    // 補充 : zBox[index]表示：從位置 index 開始的子字串與整個字串 s 的最長公共前綴長度
    // 例如 : s="ababab", zBox[2]=4 表示從位置2開始的 "abab" 與開頭的 "abab" 有 4 個字元匹配
    int[] zBox = new int[searchLength];

    // 3. 初始化 zBox 陣列
    // 目的： Z 字串演算法要將所有陣列的匹配長度找出
    int zBoxLeft = 0, zBoxRight = 0;

    // 4. 計算 zBox 陣列 從位置 1 開始（位置 0 可跳過，自己跟自己）
    for (int index = 1; index < searchLength; index++)
    {
        // 5-1. Index 在 zBox 之外 (index > zBoxRight)
        if (index > zBoxRight)
        {
            // 5-1-1. 當前位置在已知匹配區間之外，需要重新暴力比對
            zBoxLeft = zBoxRight = index;  // 將新的匹配區間起點設為 i

            // 5-1-2. 進行逐一匹配
            MatchAndSetArray(ref zBox, ref index, ref zBoxLeft, ref zBoxRight);

        }
        // 5-2. Index 在 Z-box 之內
        else
        {
            // 5-2-1. 當前位置在已知匹配區間內，可以利用之前計算出的 zBox 信息
            int offsetIndex = index - zBoxLeft;

            // 5-2-2. 可重用 : zBox 紀錄 (會進入此表示前一次有找到至少1個匹配)
            if (zBox[offsetIndex] < zBoxRight - index + 1)
            {
                zBox[index] = zBox[offsetIndex];
            }
            else// 5-2-3. 不可重用的狀況 
            {
                // 補充: LeetCode 不會進入此，但是 Z 演算法的完整實作必須包含它
                // 進入此的條件有以下：
                // - 1. 當 pattern 長度小於 text 時
                // - 2. 且存在重複或週期性結構       
                // 例如: pattern = "aaa", text = "aaaa"
                zBoxLeft = index;

                // 5-2-4. 進入匹配
                MatchAndSetArray(ref zBox,ref index, ref zBoxLeft, ref zBoxRight);
            }
        }
    }

    // 6-1. 檢查是否完全匹配 - 有目標數量表示有完全匹配
    for (int index = modelLength + 1; index < searchLength; index++)
    {
        if (zBox[index] == modelLength)
        {
            return true;
        }
    }
    return false;//6-2. 沒找到

    // 找出匹配量，並更新 zBox 陣列
    void MatchAndSetArray(ref int[] array, ref int zBoxIndex,
        ref int zBoxLeft, ref int zBoxRight)
    {
        // 1. 匹配
        while (zBoxRight < searchLength &&
               searchStr[zBoxRight - zBoxLeft] == searchStr[zBoxRight])
        {
            zBoxRight++;
        }

        // 2. 記錄匹配長度
        array[zBoxIndex] = zBoxRight - zBoxLeft;

        // 3. 因為 while 迴圈會讓 zBoxRight 多加 1，因此要減 1 校正
        zBoxRight--;
    }
}

Step 2：LeetCode 上的執行方式

public bool RotateString(string s, string goal)
{
    if (s.Length != goal.Length)
    {
        return false;
    }                      
    return ZAlgorithmSearch(s+s, goal);
}

Step 3：LeetCode - 成功執行結果

附上此代碼確實可在 LeetCode 上執行 C# 版本
※此LeetCode 題目相當簡單，使用 z 演算法會徒增記憶耗費，此範例展示此演算法是可以實際應用

Runtime 範圍	0 ms
Runtime Best Beat	100.00%
Memory 範圍	40.76 ~ 40.78 MB
Memory Best Beat	72.97%

Step 4：補充 LeetCode 標準解法

實際上面對題目時應妥善利用 C# 內建的函式庫，用聰明的方式處理問題。

public bool RotateString(string s, string goal)
{
    if (s.Length != goal.Length)
    {
        return false;
    }                      
    return return (s+s).Contains(goal);
}

第三部分：Z 演算法 - 圖解

Step 1：準備階段 - 資料預處理

以 LeetCode 的範例做說明

文本	：	abcde
搜尋字串	：	cdeab

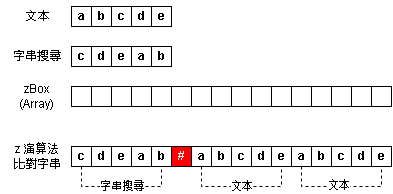
Step 2：預處理階段

以下為預處理資料

文本	：	abcde
搜尋字串	：	cdeab
zBox(Array)	：	int[16] 依照 zBox 比對字串長度
zBox比對字串	：	cdeab#abcdeabcde

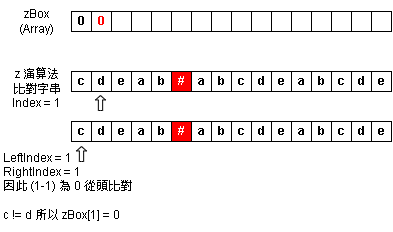
Step 3：zBox Index = 1

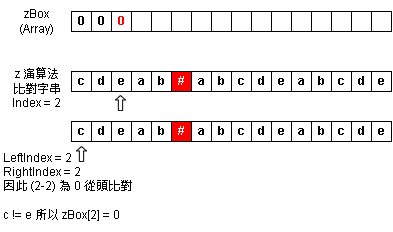
Step 4：zBox Index = 2

Step 5：zBox Index = 3~8

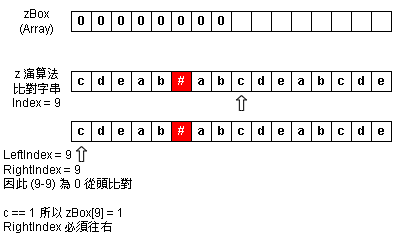
Step 6：zBox Index = 9 - 匹配到相同

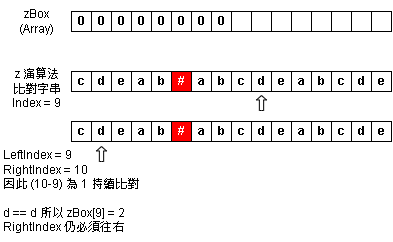
Step 7：zBox Index = 9 - 持續匹配

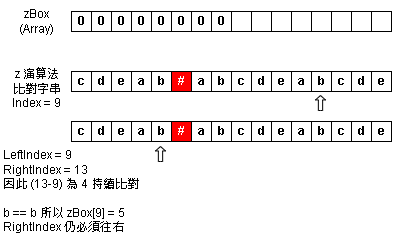
Step 8：zBox Index = 9 - 匹配結束紀錄

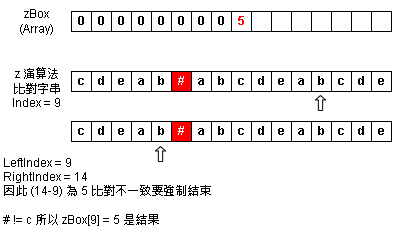
Step 9：zBox Index = 10 - 小於 RightIndex 狀況

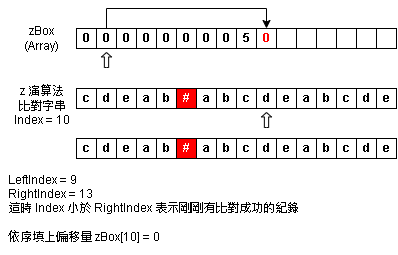
Step 10：zBox Index = 10~13 - 補完偏移量

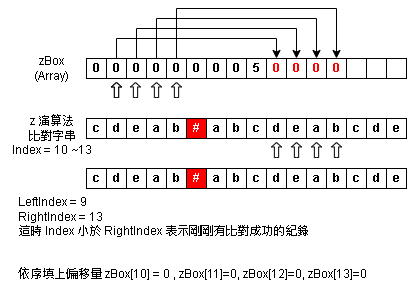
Step 11：zBox Index = 14 - 匹配到相同

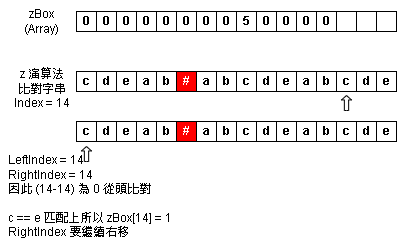
Step 12：zBox Index = 14 - 匹配結束紀錄

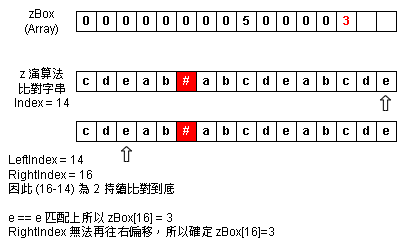
Step 13：zBox Index = 15,16 - 補完偏移量

Step 14：完成 zBox Array

最終我們可以得到 zBox[8] = 5 與搜尋字串長度(5) 相同，對應 LeetCode 的返回為 True

文本	：	abcde
搜尋字串	：	cdeab
zBox(Array)	：	int[16] {0,0,0,0,0,0,0,0,5,0,0,0,0,3,0,0}