0094. ASP.NET Core 中實現 Keccak-256 雜湊演算法

日期：2025年 05月 17日

標籤： C# Keccak Asp.NET Core Windows Forms Nethereum Util Portable BouncyCastle

摘要：C# 學習筆記

應用所需：1. Visual Studio 2022 以上，支援 .net Core 8.0 以上
範例專案：Keccak-256 4.2.9 反組譯範例代碼
基本介紹：本篇分為四大部分。
第一部分：Keccak-256 介紹
第二部分：現有 C# 庫比較
第三部分：介紹 Nethereum Util Library
第四部分：Demo 驗證成果

第一部分：Keccak-256 介紹

Step 1：歷史背景

演算法由密碼學家團隊 Guido Bertoni、Joan Daemen、Michaël Peeters 和 Gilles Van Assche 開發。
這個團隊在2008年首次提出了Keccak作為NIST（美國國家標準與技術研究院）SHA-3密碼雜湊演算法競賽的候選者。

在2012年10月，經過多年的公開評估和分析，NIST最終選擇Keccak作為SHA-3標準的獲勝演算法。這一選擇主要基於Keccak的創新設計、安全性和效能特性。
值得注意的是，Keccak與之前的SHA家族（SHA-1、SHA-2）有著根本性的設計差異，這使得它不容易受到針對早期演算法的攻擊。

雖然Keccak成為了SHA-3的基礎，但標準化過程中NIST對原始Keccak做了一些修改。
因此，Keccak-256和SHA3-256雖然非常相似，但在詳細實現上存在細微差別。
特別是在以太坊區塊鏈中使用的是原始的Keccak-256版本，而不是標準化的SHA3-256。

簡言之，Keccak-256 與 SHA3-256 不同，主要用在以太坊區塊鏈中使用，錢包、合約

Step 2：主要用途

Keccak-256的應用非常廣泛，除了以太坊區塊鏈中使用，還包括：

1. 區塊鏈技術	：	最廣為人知的應用是在以太坊區塊鏈中，Keccak-256用於地址生成、交易、智能合約
2. 資料完整性驗證	：	驗證檔案或訊息在傳輸過程中沒有被修改
3. 密碼儲存	：	作為密碼雜湊函數的組成部分（通常與加鹽和迭代技術結合）
4. 隨機數生成	：	作為偽隨機數生成器的組成部分
5. 數位簽章方案	：	作為數位簽章演算法的組成部分

Step 3：特色 & 注意事項

Keccak-256具有幾個關鍵特性，使其在各種應用中脫穎而出：

1. 抗碰撞性	：	找到兩個產生相同雜湊值的不同輸入在計算上是不可行的
2. 抗原像性	：	給定雜湊值，找到能產生該雜湊的輸入在計算上是不可行的
3. 抵抗攻擊	：	設計上能抵抗已知的攻擊方法，包括長度擴展攻擊（這是影響早期SHA演算法的漏洞）
4. 效能優異	：	在各種硬體平台上都能高效實現，包括資源受限的設備
5. 設計靈活	：	基礎構造允許不同的安全參數和輸出長度

使用時注意以下幾點即可使用：

1. 輸入編碼：確保一致的輸入編碼（UTF-8、ASCII等），因為即使是微小的輸入變化也會產生完全不同的雜湊結果

2. 不同的實現：注意區分標準SHA3-256和原始Keccak-256，特別是在與以太坊相關的應用中

3. 安全更新：保持關注密碼學社群可能發現的任何潛在弱點或攻擊性

第二部分：現有 C# 庫比較

Step 1：支援於 Asp.net Core 下的庫比較

若要在 Asp.net Core 中使用，目前有支援 Keccak 的有以下 2 個
BouncyCastle 與 Nethereum.Util

比較面向	BouncyCastle	Nethereum.Util
實現類名	`KeccakDigest`	`Sha3Keccack` (注意 4.2.9 官方 Source Code 拼寫錯誤)
用途範圍	通用密碼學庫，支援多種演算法	專為以太坊區塊鏈開發設計
支援輸出大小	224、256、384、512 位	主要支援 256 位 (以太坊使用)
API 風格	傳統密碼學風格，分步驟執行	簡潔單一方法調用
記憶體使用	支援流式處理，適合大檔案	一次性處理，較適合小到中等量資料
庫體積	較大，完整密碼學套件	較小，專注以太坊所需功能
依賴關係	獨立，無外部依賴	屬於 Nethereum 生態系統
社群支持	成熟，廣泛應用於多領域	活躍於以太坊開發社群
維護頻率	定期更新，安全修補	隨以太坊協議演化更新
文檔品質	全面但技術性強	偏向實用，區塊鏈開發者友善
效能特性	高度優化但通用	針對以太坊使用場景優化
標準合規性	嚴格遵循原始 Keccak 規範	符合以太坊實現要求
整合優勢	與其他密碼學功能整合便利	與以太坊工具鏈緊密整合
適用場景	需要多種密碼學演算法大檔案處理標準密碼學應用	以太坊開發智能合約相關功能輕量級區塊鏈應用
NuGet 包	`Portable.BouncyCastle`	`Nethereum.Util`

如果用於研究、完整性可以選擇 BouncyCastle
如果只用於以太坊區塊鏈，可以選擇輕量化的 Nethereum.Util

Step 2：安裝 BouncyCastle

Nuget -> 找尋 BouncyCastle.Cryptography 進行安裝

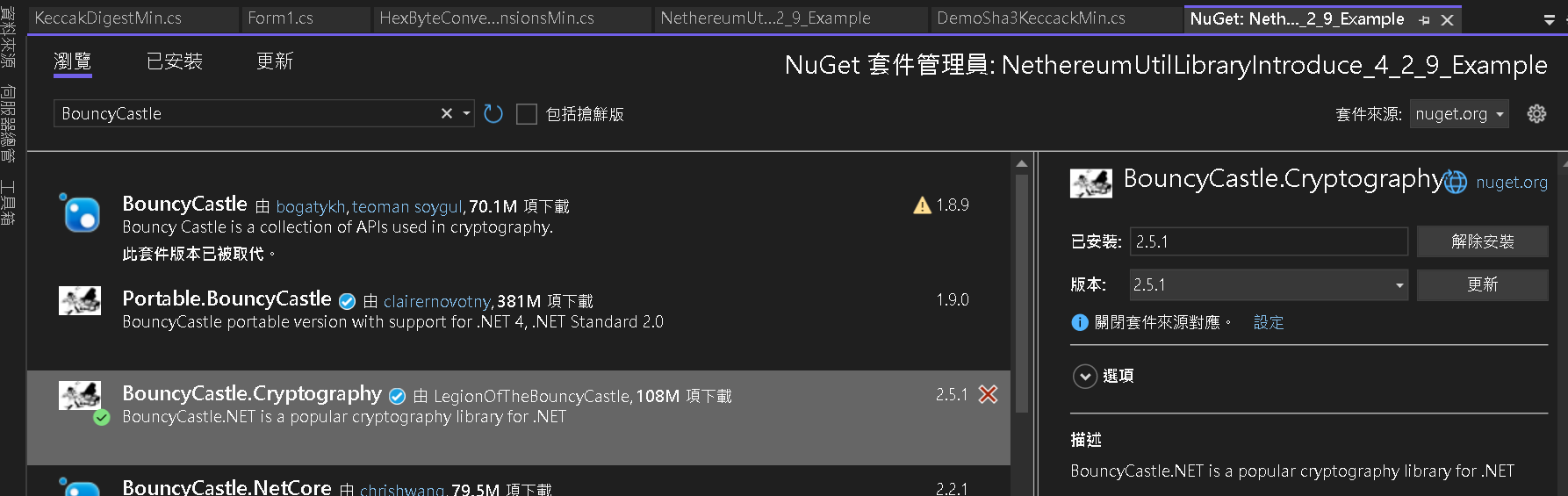
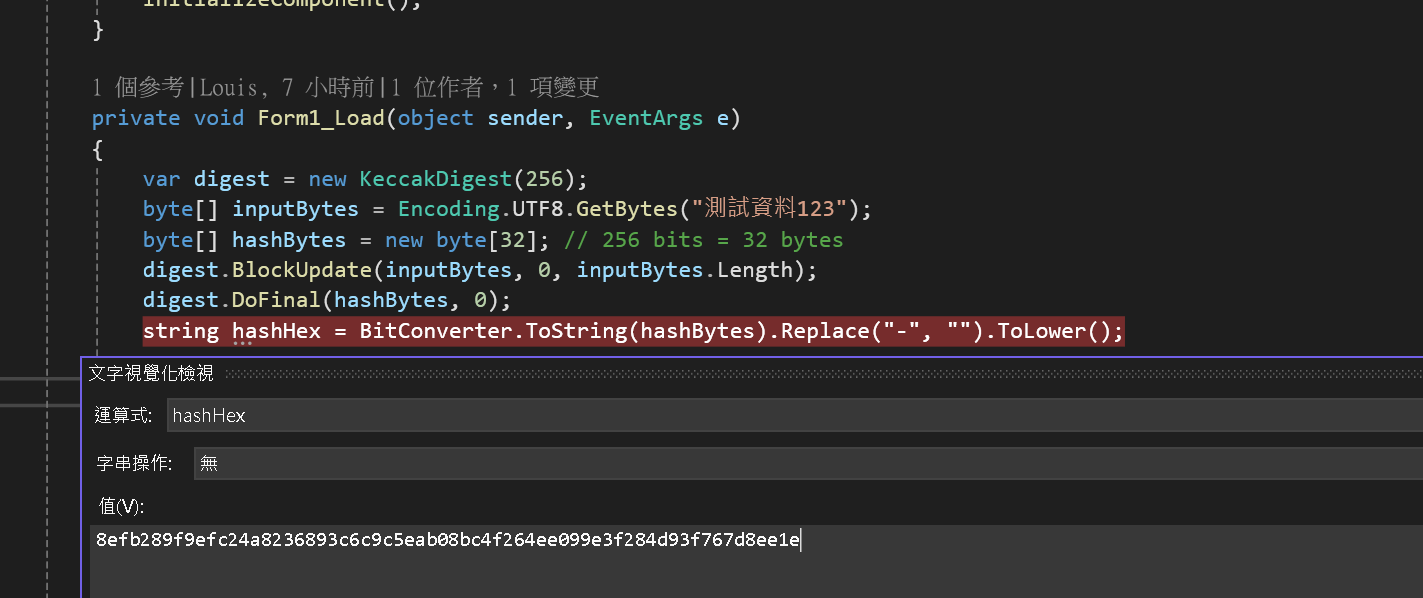
Step 3：測試 BouncyCastle Keccak-256 產生雜湊

這邊範例都使用字串 測試資料123 ，可以得到雜湊 Hash

8efb289f9efc24a8236893c6c9c5eab08bc4f264ee099e3f284d93f767d8ee1e

範例代碼：

  var digest = new KeccakDigest(256);
  byte[] inputBytes = Encoding.UTF8.GetBytes("測試資料123");
  byte[] hashBytes = new byte[32]; // 256 bits = 32 bytes
  digest.BlockUpdate(inputBytes, 0, inputBytes.Length);
  digest.DoFinal(hashBytes, 0);
  string hashHex = BitConverter.ToString(hashBytes).Replace("-", "").ToLower();

<br

Step 4：安裝 Nethereum.Util

Nuget -> 找尋 Nethereum.Util 進行安裝

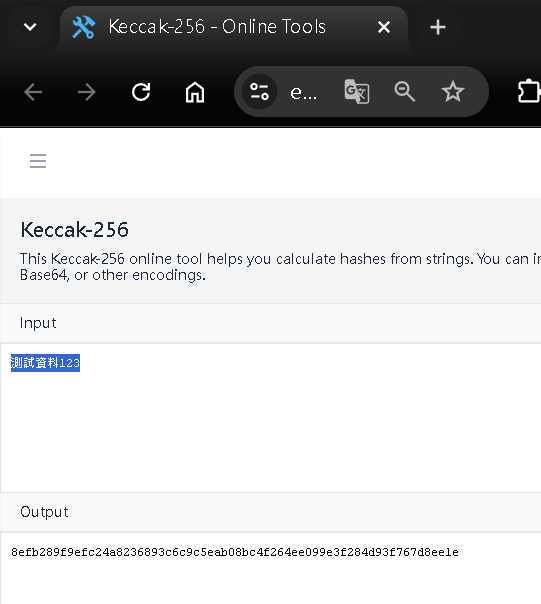
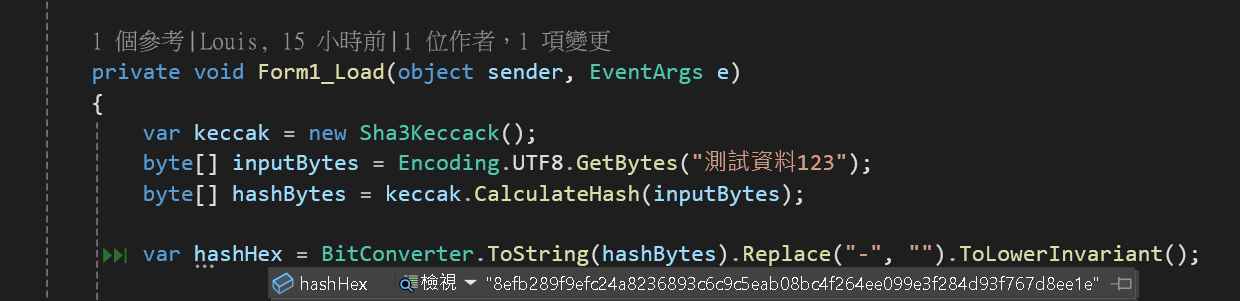
Step 3：測試 Nethereum.Util Keccak-256 雜湊

這邊範例都使用字串 測試資料123 ，可以得到 Hash

但代碼更精簡了

8efb289f9efc24a8236893c6c9c5eab08bc4f264ee099e3f284d93f767d8ee1e

範例代碼：

var keccak = new Sha3Keccack();
byte[] inputBytes = Encoding.UTF8.GetBytes("測試資料123");
byte[] hashBytes = keccak.CalculateHash(inputBytes);
var hashHex = BitConverter.ToString(hashBytes).Replace("-", "").ToLowerInvariant();

第三部分：介紹 Nethereum Util Library

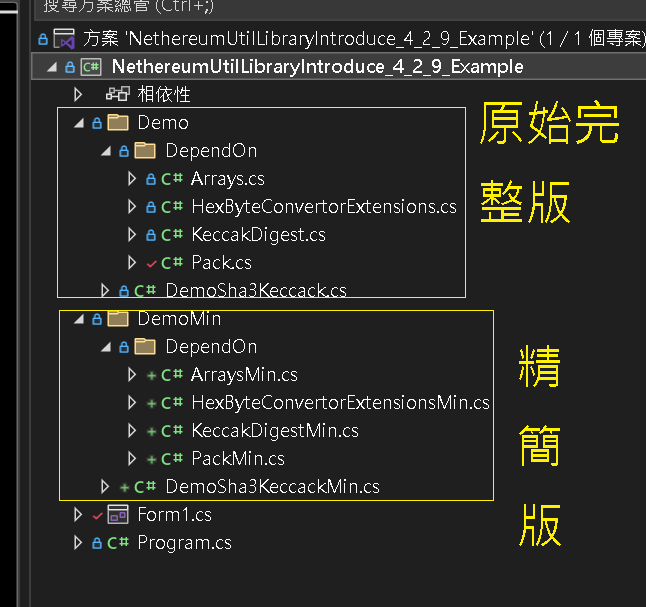
Step 1：範例專案架構

打開範例專案：Keccak-256 4.2.9 反組譯範例代碼有 2 個部分，代碼來源於
代碼來源於開源 Nethereum，並且 Nuget 上安裝的庫來源於此

完整版	深入探查每個 `Sha3Keccack` 裡面的方法
精簡版	實現 `Sha3Keccack` 時，有用到的參考，移除未使用在 Keccack 算法的 Method

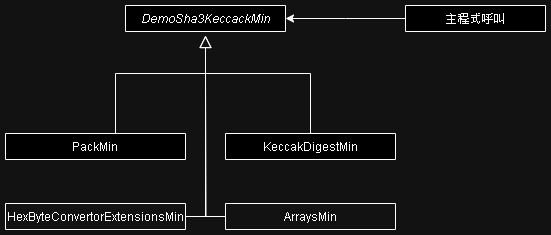
Step 2：精簡版架構

此專案代碼架構如圖，主要由 主程式 呼叫主類庫 DemoSha3KeccackMin
有關係的相互依賴

Step 3：主程式叫用

textBoxInput.Text 為主要輸入的字串變數，通常引用 Nethereum.Util 後，都是這樣使用。

/// <summary>
/// 執行 Hash Compute
/// </summary>        
private void button1_Click(object sender, EventArgs e)
{
    var result = string.Empty;
    try
    { 
        // 建立 Sha3Keccack 類別的實例，用於計算 Keccak-256 雜湊值
        var keccak = new DemoSha3KeccackMin();

        // 將輸入字串轉換為 UTF-8 編碼的位元組陣列
        byte[] bytes = Encoding.UTF8.GetBytes(textBoxInput.Text);

        // 使用 Keccak 演算法計算輸入位元組陣列的雜湊值
        byte[] hash = keccak.CalculateHash(bytes);

        // 將雜湊結果轉換為小寫的十六進制字串表示形式，並移除分隔符號 "-"
        result = BitConverter.ToString(hash).Replace("-", "").ToLower();
    }
    catch
    {
        // 異常處理：當 Nethereum.Util.Sha3Keccack 類庫執行發生問題時，
        // 由於該類別未實現 IDisposable 介面，無法正確釋放資源，因此選擇捨棄結果並返回空字串
    }
    textBoxOutput.Text = result;
}

Step 4：DemoSha3KeccackMin

實現了 Keccak-256 雜湊演算法的工具類別，常用於以太坊相關的密碼學操作。
亦是入口點

/// <summary>
/// 介紹 Nethereum.Util.Sha3Keccack 版本 4.2.9 的代碼
/// <para>如何進行產生雜湊</para>
/// </summary>
public class DemoSha3KeccackMin
{
    /// <summary>
    /// 核心方法：計算位元組陣列的 Keccak-256 雜湊值
    /// </summary>
    /// <param name="value">要計算雜湊的位元組陣列</param>
    /// <returns>雜湊結果的位元組陣列</returns>
    public byte[] CalculateHash(byte[] value)
    {
        // 建立一個 256 位元的 KeccakDigest 物件
        KeccakDigestMin keccakDigest = new KeccakDigestMin(256);
        // 建立一個與摘要大小相同的位元組陣列來存放結果
        byte[] array = new byte[keccakDigest.GetDigestSize()];
        // 將輸入資料更新到雜湊計算中
        keccakDigest.BlockUpdate(value, 0, value.Length);
        // 完成雜湊計算並將結果寫入輸出陣列
        keccakDigest.DoFinal(array, 0);
        return array;
    }
}

Step 5：PackMin

提供了一系列用於處理整數與位元組陣列之間轉換的靜態方法，特別關注於大端序(Big-Endian, BE)和小端序(Little-Endian, LE)的轉換。
這些方法在密碼學演算法 Keccak 中扮演重要角色。

public sealed class PackMin
{
    /// <summary>
    /// 私有建構函式，防止類別被實例化，僅提供靜態方法使用
    /// </summary>
    private PackMin()
    {
    }

    // ===================== 大端序 (Big-Endian, BE) 轉換方法 =====================

    /// <summary>
    /// 將 32位元無符號整數 轉換為 大端序位元組陣列
    /// </summary>
    /// <param name="n">要轉換的 32 位元整數</param>
    /// <param name="bs">用於存儲結果的位元組陣列</param>
    internal static void UInt32_To_BE(uint n, byte[] bs)
    {
        bs[0] = (byte)(n >> 24);  // 取最高 8 位 (位元組 3)
        bs[1] = (byte)(n >> 16);  // 取次高 8 位 (位元組 2)
        bs[2] = (byte)(n >> 8);   // 取次低 8 位 (位元組 1)
        bs[3] = (byte)n;          // 取最低 8 位 (位元組 0)
    }
  
    // ===================== 小端序 (Little-Endian, LE) 轉換方法 =====================

    /// <summary>
    /// 將 32位元無符號整數 轉換為 小端序位元組陣列，並寫入指定偏移位置
    /// </summary>
    /// <param name="n">要轉換的 32 位元整數</param>
    /// <param name="bs">用於存儲結果的位元組陣列</param>
    /// <param name="off">寫入的起始位置偏移量</param>
    internal static void UInt32_To_LE(uint n, byte[] bs, int off)
    {
        bs[off] = (byte)n;              // 取最低 8 位
        bs[off + 1] = (byte)(n >> 8);   // 取次低 8 位
        bs[off + 2] = (byte)(n >> 16);  // 取次高 8 位
        bs[off + 3] = (byte)(n >> 24);  // 取最高 8 位
    }


    /// <summary>
    /// 從小端序位元組陣列的指定偏移位置轉換 32位元無符號整數
    /// </summary>
    /// <param name="bs">小端序格式的位元組陣列</param>
    /// <param name="off">讀取的起始位置偏移量</param>
    /// <returns>轉換後的 32 位元整數</returns>
    internal static uint LE_To_UInt32(byte[] bs, int off)
    {
        return (uint)(bs[off] | (bs[off + 1] << 8) |
                     (bs[off + 2] << 16) | (bs[off + 3] << 24));
    }

    /// <summary>
    /// 將 64位元無符號整數 轉換為 小端序位元組陣列，並寫入指定偏移位置
    /// </summary>
    /// <param name="n">要轉換的 64 位元整數</param>
    /// <param name="bs">用於存儲結果的位元組陣列</param>
    /// <param name="off">寫入的起始位置偏移量</param>
    internal static void UInt64_To_LE(ulong n, byte[] bs, int off)
    {
        UInt32_To_LE((uint)n, bs, off);            // 低 32 位
        UInt32_To_LE((uint)(n >> 32), bs, off + 4); // 高 32 位
    }

    /// <summary>
    /// 將 64位元無符號整數陣列 轉換為 小端序位元組陣列，並寫入指定偏移位置
    /// </summary>
    /// <param name="ns">要轉換的 64 位元整數陣列</param>
    /// <param name="bs">用於存儲結果的位元組陣列</param>
    /// <param name="off">寫入的起始位置偏移量</param>
    internal static void UInt64_To_LE(ulong[] ns, byte[] bs, int off)
    {
        for (int i = 0; i < ns.Length; i++)
        {
            UInt64_To_LE(ns[i], bs, off);  // 逐個轉換並寫入
            off += 8;                       // 每個 ulong 後移 8 位元組
        }
    }

    /// <summary>
    /// 將 64位元無符號整數陣列的指定部分 轉換為 小端序位元組陣列，並寫入指定偏移位置
    /// </summary>
    /// <param name="ns">要轉換的 64 位元整數陣列</param>
    /// <param name="nsOff">整數陣列的起始位置</param>
    /// <param name="nsLen">要轉換的整數數量</param>
    /// <param name="bs">用於存儲結果的位元組陣列</param>
    /// <param name="bsOff">位元組陣列的起始寫入位置</param>
    internal static void UInt64_To_LE(ulong[] ns, int nsOff, int nsLen, byte[] bs, int bsOff)
    {
        for (int i = 0; i < nsLen; i++)
        {
            UInt64_To_LE(ns[nsOff + i], bs, bsOff);  // 轉換指定位置的整數並寫入
            bsOff += 8;                              // 每個 ulong 後移 8 位元組
        }
    }

    /// <summary>
    /// 從小端序位元組陣列的指定偏移位置轉換 64位元無符號整數
    /// </summary>
    /// <param name="bs">小端序格式的位元組陣列</param>
    /// <param name="off">讀取的起始位置偏移量</param>
    /// <returns>轉換後的 64 位元整數</returns>
    internal static ulong LE_To_UInt64(byte[] bs, int off)
    {
        uint num = LE_To_UInt32(bs, off);                    // 取低 32 位
        return ((ulong)LE_To_UInt32(bs, off + 4) << 32) | num; // 高 32 位左移後與低 32 位合併
    }
}

Step 6：KeccakDigestMin

核心: Keccak 雜湊函數的核心實現類別

// 3-2. KeccakDigest
/// <summary>
/// Keccak 雜湊函數的核心實現類別
/// Keccak 是 SHA-3 雜湊函數家族的基礎演算法，此實現特別用於以太坊中的 Keccak-256
/// </summary>
public class KeccakDigestMin
{
    /// <summary>
    /// Keccak 輪常數陣列，用於每輪的 Iota 步驟
    /// </summary>
    private static readonly ulong[] KeccakRoundConstants = KeccakInitializeRoundConstants();

    /// <summary>
    /// Keccak 位元偏移量陣列，用於 Rho 步驟中的位元旋轉操作
    /// </summary>
    private static readonly int[] KeccakRhoOffsets = KeccakInitializeRhoOffsets();

    /// <summary>
    /// Keccak 狀態陣列的長度（位元組數），固定為 200 位元組 (1600 位元)
    /// </summary>
    private static readonly int STATE_LENGTH = 200;

    /// <summary>
    /// Keccak 的內部狀態，以 64 位元無符號整數陣列表示（25 個 64 位元值 = 1600 位元）
    /// </summary>
    private ulong[] state = new ulong[STATE_LENGTH / 8];

    /// <summary>
    /// 資料佇列，用於存儲待處理的輸入資料
    /// </summary>
    protected byte[] dataQueue = new byte[192];

    /// <summary>
    /// 速率值，定義了每個吸收階段可處理的位元數
    /// </summary>
    protected int rate;

    /// <summary>
    /// 目前在資料佇列中的位元數
    /// </summary>
    protected int bitsInQueue;

    /// <summary>
    /// 雜湊輸出的固定長度（位元數）
    /// </summary>
    protected int fixedOutputLength;

    /// <summary>
    /// 標記是否處於擠壓階段
    /// </summary>
    protected bool squeezing;

    /// <summary>
    /// 擠壓階段可用的位元數
    /// </summary>
    protected int bitsAvailableForSqueezing;

    /// <summary>
    /// 初始化 Keccak 輪常數
    /// 這些常數用於 Keccak 排列函數的 Iota 步驟
    /// </summary>
    /// <returns>包含 24 個輪常數的陣列</returns>
    private static ulong[] KeccakInitializeRoundConstants()
    {
        ulong[] array = new ulong[24];
        byte b = 1;
        for (int i = 0; i < 24; i++)
        {
            array[i] = 0uL;
            for (int j = 0; j < 7; j++)
            {
                int num = (1 << j) - 1;
                if (((uint)b & (true ? 1u : 0u)) != 0)
                {
                    array[i] ^= (ulong)(1L << num);
                }

                bool flag = (b & 0x80) != 0;
                b <<= 1;
                if (flag)
                {
                    b = (byte)(b ^ 0x71u);
                }
            }
        }

        return array;
    }

    /// <summary>
    /// 初始化 Keccak Rho 偏移量
    /// 這些偏移量用於 Keccak 排列函數的 Rho 步驟中的旋轉操作
    /// </summary>
    /// <returns>包含 25 個偏移量的陣列</returns>
    private static int[] KeccakInitializeRhoOffsets()
    {
        int[] array = new int[25];
        int num = (array[0] = 0);
        int num2 = 1;
        int num3 = 0;
        for (int i = 1; i < 25; i++)
        {
            num = (num + i) & 0x3F;
            array[num2 % 5 + 5 * (num3 % 5)] = num;
            int num4 = num3 % 5;
            int num5 = (2 * num2 + 3 * num3) % 5;
            num2 = num4;
            num3 = num5;
        }

        return array;
    }

    /// <summary>
    /// 以指定位元長度建構 Keccak 摘要器
    /// </summary>
    /// <param name="bitLength">雜湊結果的位元長度，必須是 128、224、256、288、384 或 512 之一</param>
    public KeccakDigestMin(int bitLength)
    {
        Init(bitLength);
    }



    /// <summary>
    /// 獲取摘要大小（位元組數）
    /// </summary>
    /// <returns>雜湊結果的位元組數</returns>
    public virtual int GetDigestSize()
    {
        return fixedOutputLength >> 3;  // 將位元數轉換為位元組數（除以 8）
    }


    /// <summary>
    /// 更新摘要器狀態，吸收位元組陣列的指定部分
    /// </summary>
    /// <param name="input">輸入位元組陣列</param>
    /// <param name="inOff">起始偏移量</param>
    /// <param name="len">長度</param>
    public virtual void BlockUpdate(byte[] input, int inOff, int len)
    {
        Absorb(input, inOff, len);
    }

    /// <summary>
    /// 完成雜湊計算並將結果寫入輸出陣列
    /// </summary>
    /// <param name="output">輸出位元組陣列</param>
    /// <param name="outOff">輸出偏移量</param>
    /// <returns>寫入的位元組數</returns>
    public virtual int DoFinal(byte[] output, int outOff)
    {
        Squeeze(output, outOff, fixedOutputLength >> 3);
        Reset();
        return GetDigestSize();
    }

    /// <summary>
    /// 重置摘要器狀態
    /// </summary>
    public virtual void Reset()
    {
        Init(fixedOutputLength);
    }

    /// <summary>
    /// 初始化摘要器，設置正確的位元長度
    /// </summary>
    /// <param name="bitLength">雜湊結果的位元長度</param>
    private void Init(int bitLength)
    {
        switch (bitLength)
        {
            case 128:
            case 224:
            case 256:
            case 288:
            case 384:
            case 512:
                InitSponge(1600 - (bitLength << 1));
                break;
            default:
                throw new ArgumentException("must be one of 128, 224, 256, 288, 384, or 512.", "bitLength");
        }
    }

    /// <summary>
    /// 初始化海綿結構，設置速率和容量
    /// </summary>
    /// <param name="rate">海綿結構的速率（位元）</param>
    private void InitSponge(int rate)
    {
        // 檢查速率值是否有效 (必須是 64 的倍數且在有效範圍內)
        if (rate <= 0 || rate >= 1600 || ((uint)rate & 0x3Fu) != 0)
        {
            throw new InvalidOperationException("invalid rate value");
        }

        this.rate = rate;
        Array.Clear(state, 0, state.Length);  // 清空狀態陣列
        ArraysMin.Fill(dataQueue, 0);            // 清空資料佇列
        bitsInQueue = 0;
        squeezing = false;
        bitsAvailableForSqueezing = 0;
        fixedOutputLength = 1600 - rate >> 1;  // 容量的一半作為輸出長度
    }

    /// <summary>
    /// 吸收階段 - 將輸入資料加入狀態
    /// </summary>
    /// <param name="data">輸入資料</param>
    /// <param name="off">偏移量</param>
    /// <param name="len">長度</param>
    protected void Absorb(byte[] data, int off, int len)
    {
        // 檢查佇列中的位元是否全都是完整位元組 (8 的倍數)
        if (((uint)bitsInQueue & 7u) != 0)
        {
            throw new InvalidOperationException("attempt to absorb with odd length queue");
        }

        // 檢查是否已經處於擠壓階段
        if (squeezing)
        {
            throw new InvalidOperationException("attempt to absorb while squeezing");
        }

        int num = bitsInQueue >> 3;  // 佇列中的位元組數
        int num2 = rate >> 3;        // 速率對應的位元組數
        int num3 = 0;                // 已處理的輸入位元組數

        while (num3 < len)
        {
            // 如果佇列為空且有足夠的輸入資料，直接處理整個區塊
            if (num == 0 && num3 <= len - num2)
            {
                do
                {
                    KeccakAbsorb(data, off + num3);
                    num3 += num2;
                }
                while (num3 <= len - num2);
                continue;
            }

            // 否則，將資料添加到佇列中
            int num4 = Math.Min(num2 - num, len - num3);
            Array.Copy(data, off + num3, dataQueue, num, num4);
            num += num4;
            num3 += num4;

            // 如果佇列已滿，處理該區塊
            if (num == num2)
            {
                KeccakAbsorb(dataQueue, 0);
                num = 0;
            }
        }

        bitsInQueue = num << 3;  // 更新佇列中的位元數
    }

    
    /// <summary>
    /// 填充並切換到擠壓階段
    /// </summary>
    private void PadAndSwitchToSqueezingPhase()
    {
        // 添加填充位元 (1000...001)
        dataQueue[bitsInQueue >> 3] |= (byte)(1 << (bitsInQueue & 7));

        // 如果佇列已滿，處理該區塊
        if (++bitsInQueue == rate)
        {
            KeccakAbsorb(dataQueue, 0);
            bitsInQueue = 0;
        }

        // 處理剩餘資料
        int num = bitsInQueue >> 6;       // 完整的 64 位元塊數
        int num2 = bitsInQueue & 0x3F;    // 剩餘位元數
        int num3 = 0;                     // 已處理的位元組數

        // 處理完整的 64 位元塊
        for (int i = 0; i < num; i++)
        {
            state[i] ^= PackMin.LE_To_UInt64(dataQueue, num3);
            num3 += 8;
        }

        // 處理剩餘不足 64 位元的部分
        if (num2 > 0)
        {
            ulong num4 = (ulong)((1L << num2) - 1);
            state[num] ^= PackMin.LE_To_UInt64(dataQueue, num3) & num4;
        }

        // 添加最後的填充位元
        state[rate - 1 >> 6] ^= 9223372036854775808uL;  // 2^63

        // 執行 Keccak 排列函數
        KeccakPermutation();
        KeccakExtract();

        // 切換到擠壓階段
        bitsAvailableForSqueezing = rate;
        bitsInQueue = 0;
        squeezing = true;
    }

    /// <summary>
    /// 擠壓階段 - 提取雜湊結果
    /// </summary>
    /// <param name="output">輸出陣列</param>
    /// <param name="off">偏移量</param>
    /// <param name="len">要提取的位元組數</param>
    protected void Squeeze(byte[] output, int off, int len)
    {
        // 如果尚未進入擠壓階段，先執行填充
        if (!squeezing)
        {
            PadAndSwitchToSqueezingPhase();
        }

        long num = (long)len << 3;  // 轉換為位元數
        int num3;

        // 逐步擠出所需的位元數
        for (long num2 = 0L; num2 < num; num2 += num3)
        {
            // 如果沒有可用位元，執行 Keccak 排列函數
            if (bitsAvailableForSqueezing == 0)
            {
                KeccakPermutation();
                KeccakExtract();
                bitsAvailableForSqueezing = rate;
            }

            // 確定本次可提取的位元數
            num3 = (int)Math.Min(bitsAvailableForSqueezing, num - num2);

            // 複製到輸出陣列
            Array.Copy(dataQueue, rate - bitsAvailableForSqueezing >> 3,
                      output, off + (int)(num2 >> 3), num3 >> 3);

            // 更新可用位元數
            bitsAvailableForSqueezing -= num3;
        }
    }

    /// <summary>
    /// 將資料吸收到 Keccak 狀態中並執行一次排列函數
    /// </summary>
    /// <param name="data">輸入資料</param>
    /// <param name="off">偏移量</param>
    private void KeccakAbsorb(byte[] data, int off)
    {
        int num = rate >> 6;  // 速率對應的 64 位元塊數

        // 將資料異或進狀態
        for (int i = 0; i < num; i++)
        {
            state[i] ^= PackMin.LE_To_UInt64(data, off);
            off += 8;
        }

        // 執行 Keccak 排列函數
        KeccakPermutation();
    }

    /// <summary>
    /// 從 Keccak 狀態中提取資料
    /// </summary>
    private void KeccakExtract()
    {
        PackMin.UInt64_To_LE(state, 0, rate >> 6, dataQueue, 0);
    }

    /// <summary>
    /// Keccak 排列函數 - 執行完整的 24 輪轉換
    /// </summary>
    private void KeccakPermutation()
    {
        for (int i = 0; i < 24; i++)
        {
            Theta(state);  // θ (Theta) 步驟
            Rho(state);    // ρ (Rho) 步驟
            Pi(state);     // π (Pi) 步驟
            Chi(state);    // χ (Chi) 步驟
            Iota(state, i); // ι (Iota) 步驟
        }
    }

    /// <summary>
    /// 執行位元左旋轉操作
    /// </summary>
    /// <param name="v">要旋轉的值</param>
    /// <param name="r">旋轉的位元數</param>
    /// <returns>旋轉後的值</returns>
    private static ulong leftRotate(ulong v, int r)
    {
        return (v << r) | (v >> -r);
    }

    /// <summary>
    /// Theta (θ) 步驟 - 行與列的混合擴散
    /// </summary>
    /// <param name="A">狀態陣列</param>
    private static void Theta(ulong[] A)
    {
        // 計算每列的奇偶校驗
        ulong num = A[0] ^ A[5] ^ A[10] ^ A[15] ^ A[20];
        ulong num2 = A[1] ^ A[6] ^ A[11] ^ A[16] ^ A[21];
        ulong num3 = A[2] ^ A[7] ^ A[12] ^ A[17] ^ A[22];
        ulong num4 = A[3] ^ A[8] ^ A[13] ^ A[18] ^ A[23];
        ulong num5 = A[4] ^ A[9] ^ A[14] ^ A[19] ^ A[24];

        // 計算並應用 Theta 效果
        ulong num6 = leftRotate(num2, 1) ^ num5;
        A[0] ^= num6;
        A[5] ^= num6;
        A[10] ^= num6;
        A[15] ^= num6;
        A[20] ^= num6;

        num6 = leftRotate(num3, 1) ^ num;
        A[1] ^= num6;
        A[6] ^= num6;
        A[11] ^= num6;
        A[16] ^= num6;
        A[21] ^= num6;

        num6 = leftRotate(num4, 1) ^ num2;
        A[2] ^= num6;
        A[7] ^= num6;
        A[12] ^= num6;
        A[17] ^= num6;
        A[22] ^= num6;

        num6 = leftRotate(num5, 1) ^ num3;
        A[3] ^= num6;
        A[8] ^= num6;
        A[13] ^= num6;
        A[18] ^= num6;
        A[23] ^= num6;

        num6 = leftRotate(num, 1) ^ num4;
        A[4] ^= num6;
        A[9] ^= num6;
        A[14] ^= num6;
        A[19] ^= num6;
        A[24] ^= num6;
    }

    /// <summary>
    /// Rho (ρ) 步驟 - 位元旋轉操作
    /// </summary>
    /// <param name="A">狀態陣列</param>
    private static void Rho(ulong[] A)
    {
        // 對除 A[0] 外的所有狀態位元進行旋轉
        for (int i = 1; i < 25; i++)
        {
            A[i] = leftRotate(A[i], KeccakRhoOffsets[i]);
        }
    }

    /// <summary>
    /// Pi (π) 步驟 - 位置置換
    /// </summary>
    /// <param name="A">狀態陣列</param>
    private static void Pi(ulong[] A)
    {
        // 保存 A[1] 的值用於循環置換
        ulong num = A[1];

        // 執行位置置換
        A[1] = A[6];
        A[6] = A[9];
        A[9] = A[22];
        A[22] = A[14];
        A[14] = A[20];
        A[20] = A[2];
        A[2] = A[12];
        A[12] = A[13];
        A[13] = A[19];
        A[19] = A[23];
        A[23] = A[15];
        A[15] = A[4];
        A[4] = A[24];
        A[24] = A[21];
        A[21] = A[8];
        A[8] = A[16];
        A[16] = A[5];
        A[5] = A[3];
        A[3] = A[18];
        A[18] = A[17];
        A[17] = A[11];
        A[11] = A[7];
        A[7] = A[10];

        // 完成循環置換
        A[10] = num;
    }

    /// <summary>
    /// Chi (χ) 步驟 - 非線性變換
    /// </summary>
    /// <param name="A">狀態陣列</param>
    private static void Chi(ulong[] A)
    {
        // 每 5 個元素為一組，執行非線性變換
        for (int i = 0; i < 25; i += 5)
        {
            // 暫存每組的原始值
            ulong num = A[i] ^ (~A[1 + i] & A[2 + i]);
            ulong num2 = A[1 + i] ^ (~A[2 + i] & A[3 + i]);
            ulong num3 = A[2 + i] ^ (~A[3 + i] & A[4 + i]);
            ulong num4 = A[3 + i] ^ (~A[4 + i] & A[i]);
            ulong num5 = A[4 + i] ^ (~A[i] & A[1 + i]);

            // 更新狀態
            A[i] = num;
            A[1 + i] = num2;
            A[2 + i] = num3;
            A[3 + i] = num4;
            A[4 + i] = num5;
        }
    }

    /// <summary>
    /// Iota (ι) 步驟 - 將輪常數添加到狀態
    /// </summary>
    /// <param name="A">狀態陣列</param>
    /// <param name="indexRound">當前輪數</param>
    private static void Iota(ulong[] A, int indexRound)
    {
        // 將對應輪的常數異或進狀態的首位元素
        A[0] ^= KeccakRoundConstants[indexRound];
    }
}

Step 7：HexByteConvertorExtensionsMin

轉換 : 用於加密貨幣相關操作中的 16進位 資料轉換處理

/// <summary>
/// 提供十六進制字串與位元組陣列之間轉換的擴展方法集合
/// 這些方法主要用於加密貨幣相關操作中的資料轉換處理
/// </summary>
public static class HexByteConvertorExtensionsMin
{
    /// <summary>
    /// 表示空位元組陣列的常數
    /// </summary>
    private static readonly byte[] Empty = new byte[0];

    /// <summary>
    /// 將位元組陣列轉換為十六進制字串
    /// </summary>
    /// <param name="value">要轉換的位元組陣列</param>
    /// <param name="prefix">是否包含 "0x" 前綴，預設為 false</param>
    /// <returns>十六進制字串表示形式</returns>
    public static string ToHex(this byte[] value, bool prefix = false)
    {
        // 將每個位元組轉換為兩位十六進制數，並連接起來
        // 如需前綴，則添加 "0x"
        return string.Concat(prefix ? "0x" : "", string.Concat(
            value.Select((byte b) => b.ToString("x2")).ToArray()));
    }

    /// <summary>
    /// 檢查字串是否具有十六進制前綴 "0x"
    /// </summary>
    /// <param name="value">要檢查的字串</param>
    /// <returns>如果字串以 "0x" 開頭則返回 true，否則返回 false</returns>
    public static bool HasHexPrefix(this string value)
    {
        return value.StartsWith("0x");
    }

    /// <summary>
    /// 從字串中移除十六進制前綴 "0x"（如果存在）
    /// </summary>
    /// <param name="value">可能包含十六進制前綴的字串</param>
    /// <returns>移除前綴後的字串</returns>
    public static string RemoveHexPrefix(this string value)
    {
        return value.Substring(value.StartsWith("0x") ? 2 : 0);
    }

    /// <summary>
    /// 將十六進制字串轉換為位元組陣列的內部實現
    /// </summary>
    /// <param name="value">要轉換的十六進制字串</param>
    /// <returns>對應的位元組陣列</returns>
    private static byte[] HexToByteArrayInternal(string value)
    {
        byte[] array = null;

        // 處理空或 null 輸入
        if (string.IsNullOrEmpty(value))
        {
            array = Empty;
        }
        else
        {
            int length = value.Length;

            // 確定是否有 "0x" 前綴並跳過
            int num = (value.StartsWith("0x", StringComparison.Ordinal) ? 2 : 0);

            // 計算實際的十六進制字符數量
            int num2 = length - num;

            // 處理奇數長度的十六進制字串（前面隱含添加一個 '0'）
            bool flag = false;
            if (num2 % 2 != 0)
            {
                flag = true;
                num2++;
            }

            // 創建目標位元組陣列
            array = new byte[num2 / 2];
            int num3 = 0;

            // 處理奇數長度的特殊情況
            if (flag)
            {
                array[num3++] = FromCharacterToByte(value[num], num);
                num++;
            }

            // 每次處理兩個十六進制字符，轉換為一個位元組
            for (int i = num; i < value.Length; i += 2)
            {
                byte b = FromCharacterToByte(value[i], i, 4);     // 高四位
                byte b2 = FromCharacterToByte(value[i + 1], i + 1); // 低四位
                array[num3++] = (byte)(b | b2);                     // 合併為一個位元組
            }
        }

        return array;
    }

    /// <summary>
    /// 將十六進制字串轉換為位元組陣列
    /// </summary>
    /// <param name="value">要轉換的十六進制字串</param>
    /// <returns>對應的位元組陣列</returns>
    /// <exception cref="FormatException">如果輸入不是有效的十六進制字串</exception>
    public static byte[] HexToByteArray(this string value)
    {
        try
        {
            return HexToByteArrayInternal(value);
        }
        catch (FormatException innerException)
        {
            throw new FormatException($"String '{value}' " +
                $"could not be converted to byte array (not hex?).", innerException);
        }
    }

    /// <summary>
    /// 將單個十六進制字符轉換為對應的位元組值
    /// </summary>
    /// <param name="character">十六進制字符</param>
    /// <param name="index">字符在原始字串中的索引（用於錯誤報告）</param>
    /// <param name="shift">位移量，用於高位元組處理，默認為 0</param>
    /// <returns>轉換後的位元組值</returns>
    /// <exception cref="FormatException">如果字符不是有效的十六進制字符</exception>
    private static byte FromCharacterToByte(char character, int index, int shift = 0)
    {
        byte b = (byte)character;

        // 處理 A-F 或 a-f
        if ((64 < b && 71 > b) || (96 < b && 103 > b))
        {
            if (64 == (0x40 & b))
            {
                // 將 A-F 或 a-f 轉換為 10-15 的數值，並根據 shift 進行位移
                b = ((32 != (0x20 & b)) ? ((byte)(b + 10 - 65 << shift)) : ((byte)(b + 10 - 97 << shift)));
            }
        }
        else
        {
            // 處理 0-9
            if (41 >= b || 64 <= b)
            {
                throw new FormatException($"Character '{character}' at index '{index}' " +
                    $"is not valid alphanumeric character.");
            }

            // 將 '0'-'9' 轉換為 0-9 的數值，並根據 shift 進行位移
            b = (byte)(b - 48 << shift);
        }

        return b;
    }
}

Step 8：ArraysMin

主要負責：填充陣列資料

/// <summary>
/// 提供陣列操作的工具類別，包括陣列比較、複製、轉換等常用功能
/// 此類別作為一個工具集，提供處理各種類型陣列的實用方法
/// </summary>
public abstract class ArraysMin
{
    /// <summary>
    /// 用指定的位元組填充整個陣列
    /// </summary>
    /// <param name="buf">要填充的陣列</param>
    /// <param name="b">填充值</param>
    public static void Fill(byte[] buf, byte b)
    {
        int num = buf.Length;
        while (num > 0)
        {
            buf[--num] = b;
        }
    }
}

第四部分：Demo 驗證成果

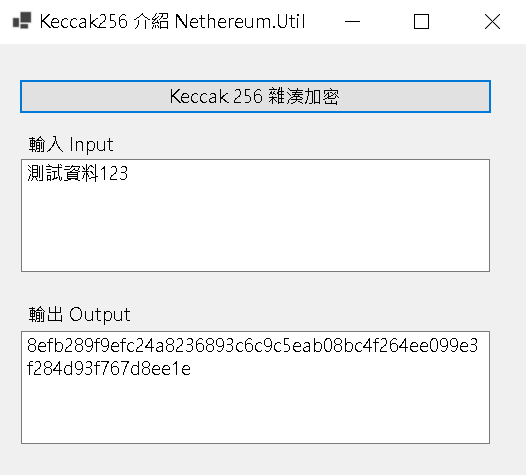
Step 1：DEMO - WinForm 執行成果

輸入字串: 測試資料123
可以得到以下結果，但仍需驗證是否與 Keaccak-256 演算法結果是否一致
接著用了 3 種不同的線上工具匹配是否一致

8efb289f9efc24a8236893c6c9c5eab08bc4f264ee099e3f284d93f767d8ee1e

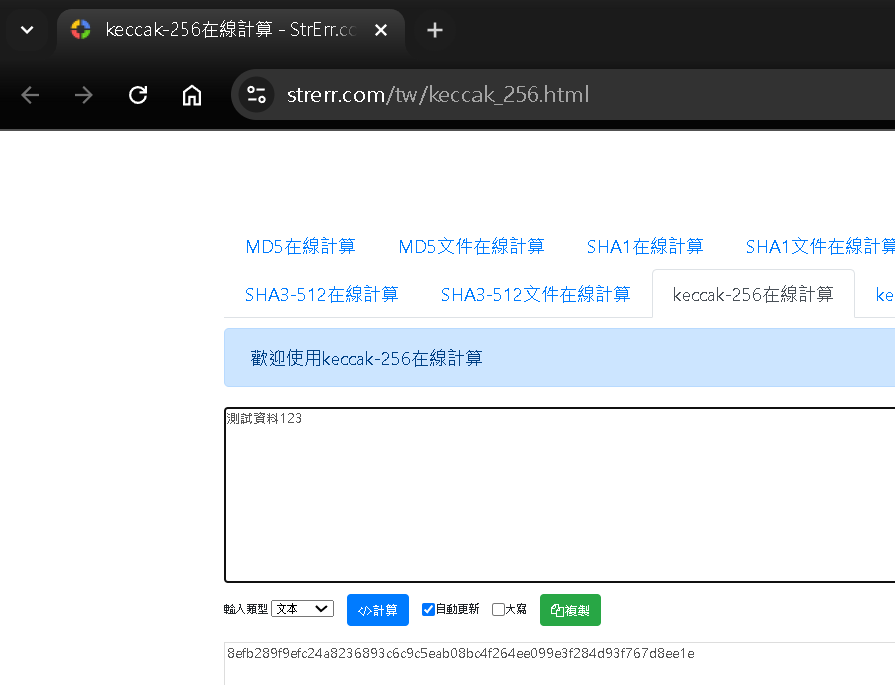
Step 2：DEMO - 線上工具1

線上工具連結，進行匹配相同字串可得到相同 Hash

Step 3：DEMO - 線上工具2

線上工具連結，進行匹配相同字串可得到相同 Hash

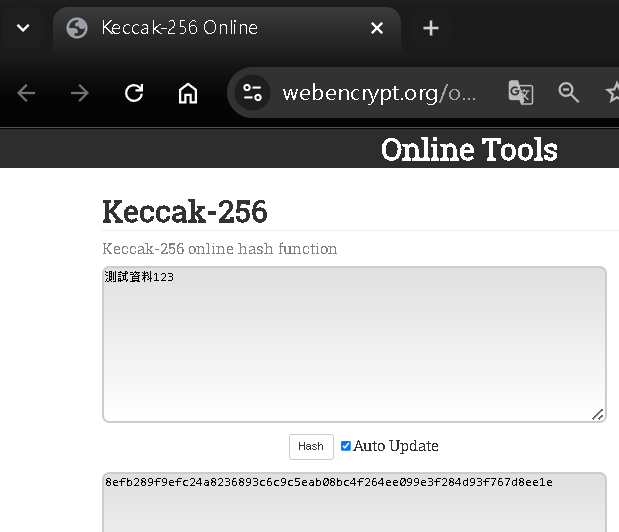
Step 4：DEMO - 線上工具3

線上工具連結，進行匹配相同字串可得到相同 Hash

目前文章總數：182 篇 最後更新：2025年 05月 31日

0094. ASP.NET Core 中實現 Keccak-256 雜湊演算法

日期：2025年 05月 17日

標籤： C# Keccak Asp.NET Core Windows Forms Nethereum Util Portable BouncyCastle

摘要：C# 學習筆記

第一部分：Keccak-256 介紹

Step 1：歷史背景

Step 2：主要用途

Step 3：特色 & 注意事項

第二部分：現有 C# 庫比較

Step 1：支援於 Asp.net Core 下的庫比較

Step 2：安裝 BouncyCastle

Step 3：測試 BouncyCastle Keccak-256 產生雜湊

Step 4：安裝 Nethereum.Util

Step 3：測試 Nethereum.Util Keccak-256 雜湊

第三部分：介紹 Nethereum Util Library

Step 1：範例專案架構

Step 2：精簡版架構

Step 3：主程式叫用

Step 4：DemoSha3KeccackMin

Step 5：PackMin

Step 6：KeccakDigestMin

Step 7：HexByteConvertorExtensionsMin

Step 8：ArraysMin

第四部分：Demo 驗證成果

Step 1：DEMO - WinForm 執行成果

Step 2：DEMO - 線上工具1

Step 3：DEMO - 線上工具2

Step 4：DEMO - 線上工具3

目前文章總數：182 篇

最後更新：2025年 05月 31日