日期：2023年 03月 26日

標籤： Algorithm Sort NoParactical Algorithm C# Asp.NET Core

摘要：演算法-排序

第一部分：堆積排序法 - 介紹

Step 1：原理

給定一組可比較陣列
1. 建構一顆Heap樹 (完全二元樹，其中每一排的節點值必定大於底下所有節點)
2-1. 遍歷該Heap樹，從最後一個節點的值開始不斷與根節點交換
2-2. 根節點與子節點做比較，大的換為根節點 (不包含剛剛替換與已替換的節點)
3. 重複2-1,2-2，直到全部走完
4. 此時這棵樹即為由小到大的排序

Step 2：演算法流程圖

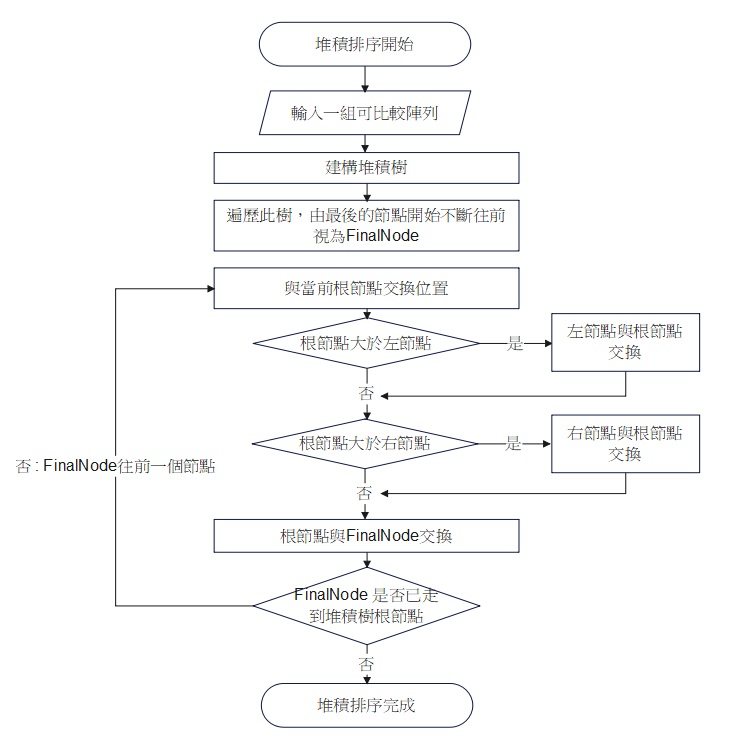
第二部分：圖解範例說明

Step 1：以整數陣列為例

初始內有7個值

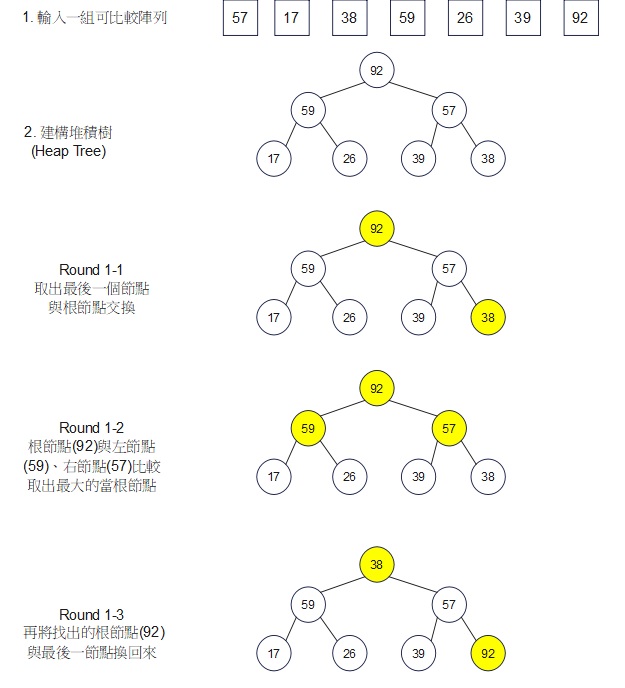
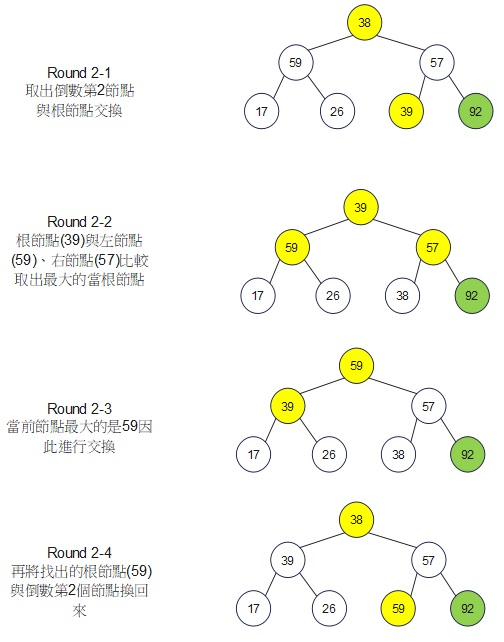
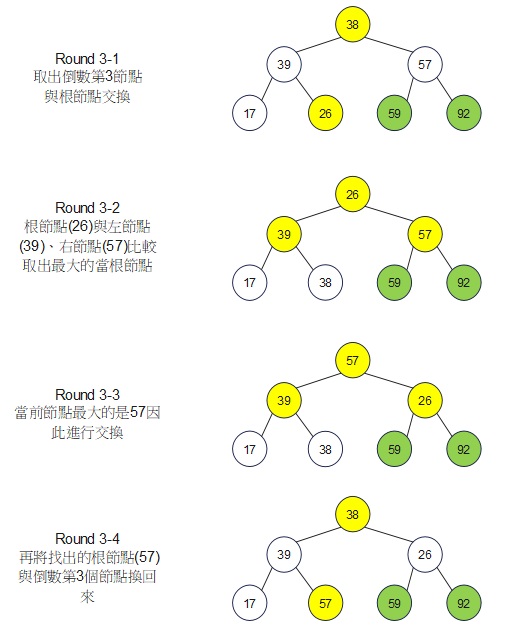
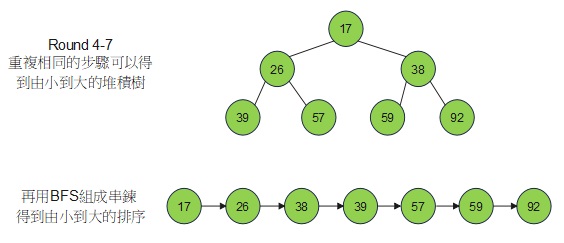
第三部分：代碼

Step 1：堆積排序法代碼 - 呼叫進入點

輸入一組數列 inputItem 求出 result

public void Execute()
{
    List<int> inputItem = new() { 57, 17, 38, 59, 26, 39, 92 };
    var heapSort = new HeapSort<int>();
    var inputArray = inputItem.ToArray();
    heapSort.HeapAscendingSort(inputItem);
}

Step 2：堆積排序法代碼 - 主程式

主要三個流程
1. 建堆積樹 (最大堆積樹)
2. 根節點與所有節點替換比較
3. 完成排序 (最小堆積樹)

public class HeapSort<T> where T : IComparable
{
    /// <summary>
    /// 堆積排序由小而大 - 主函式
    /// </summary>
    public List<T> HeapAscendingSort(List<T> items)
    {
        int maxCount = items.Count;
        //1. 建構Heap樹
        for (int index = maxCount / 2 - 1; index >= 0; index--)
        {
            HeapSorting(items, maxCount, index);
        }        //2. 遍歷所有節點，目標是根節點最小
        for (int index = maxCount - 1; index > 0; index--)
        {
            // Move current root to end
            var temp = items[0];
            items[0] = items[index];
            items[index] = temp;            //3. 不斷交換讓根節點是最小的值
            HeapSorting(items, index, 0);
        }        return items;
    }    /// <summary>
    /// 堆積排序法
    /// </summary>
    /// <param name="items"></param>
    /// <param name="maxCount"></param>
    /// <param name="currentRootIndex"></param>
    private void HeapSorting(List<T> items, int maxCount, int currentRootIndex)
    {
        int rootIndex = currentRootIndex;
        int leftNode = 2 * currentRootIndex + 1;
        int rightNode = 2 * currentRootIndex + 2;        // 探索左子節點是否更小
        if (leftNode < maxCount && items[leftNode].CompareTo(items[rootIndex]) > 0)
            rootIndex = leftNode;        // 探索右子節點是否更小
        if (rightNode < maxCount && items[rightNode].CompareTo(items[rootIndex]) > 0)
            rootIndex = rightNode;        // 發現更小的子節點->做交換位置
        if (rootIndex != currentRootIndex)
        {
            var swap = items[currentRootIndex];
            items[currentRootIndex] = items[rootIndex];
            items[rootIndex] = swap;            // 因為當前根節點異動，所以連動底下子節點
            HeapSorting(items, maxCount, rootIndex);
        }
    }
}